Graph algorithms offer algorithmic solutions to many problems in basic sciences, engineering, and social sciences.
There are many approximation methods that traverse the graph; two of the important ones are called DFS(Depth-First Search) and BFS(Breadth-First Search) for short. And it can be said that most of the algorithms developed on the graph are based on these approximation methods.

DFS(Depth-First Search) Method
It starts from an edge of the starting node to travel on the graph and continues to the farthest node that can be reached over that edge.
However, if there are nodes that cannot be reached while moving forward in this way, as in the recursive program behavior, one goes back and goes from that node to the next node in the sequence.

BFS(Breadth-First Search) Method
In this method, it starts by going from the starting node to all the neighboring nodes that can be reached. Intermediate nodes are also treated as the starting node; When an intermediate node is reached, it goes to all the neighboring and previously unvisited nodes. Then, it moves to the next node and from there to all the neighboring nodes that have not been visited before.

Greedy Approach
It is the making decision/selection method used to determine the next node while traveling the graph in order to find the optimum result or the best result on a certain subject.
In the Greedy approach, chooses the best one among the current options; criteria are made according to regional/local evaluations and it is predicted that the chosen one will be the best choice for the whole system globally.
The key word in the Greedy approach is to make a local decision to move to the next step, the next node; that is, the best one is chosen as far as the current node can be seen.
Shortest Path
Finding the shortest path is basically a problem of determining the existence of a path that can be traveled between two nodes with the least cost.
Many algorithms have been developed to determine the shortest paths from any node to all other nodes or from each node to all other nodes.
Dijkstra’s Algorithm
Dijkstra’s algorithm is an algorithm that determines the shortest path relative to a given starting point; It determines the shortest path from one node, that is, from the starting node, to all other nodes.
Time complexity is typically calculated as O(M logN).

Minimum Spanning Trees
A path tree is a tree-like path spanning all nodes on a graph; Since it is a tree feature, it does not contain closed loops. There can be more than one path tree on a graph; is called the minimum spanning tree with the least cost.
Many algorithms have been developed to determine the minimum spanning tree. Kruskal’s and Prim’s algorithms are the first ones that come to mind.
Kruskal’s Algorithm
Kruskal’s algorithm is used to determine the minimum spanning tree; its algorithmic expression is behaviorally quite simple; however, some auxiliary functions are required to perform it. The nodes on the graph are considered as N independent clusters with no connection between them; that is, there are N clusters and each cluster contains one different node at the beginning. Then, these clusters are joined to the edges with the least cost one by one to form a single cluster with a connection between the nodes. The cluster aggregation process starts from the edges with the least cost; then the least costly one among the remaining edges is chosen.

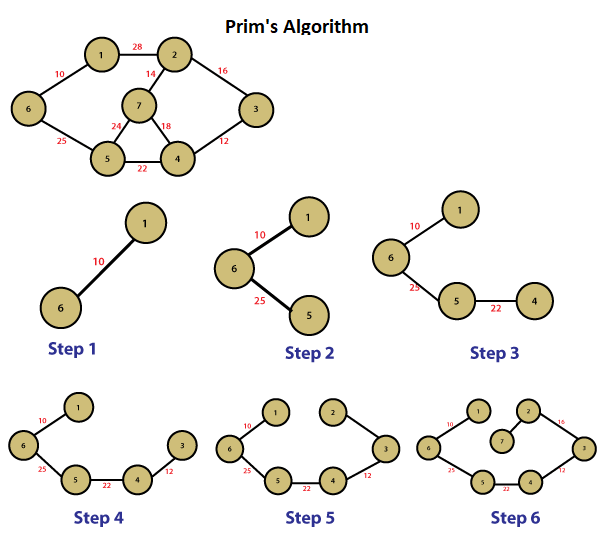
Prim’s Algorithm
Prim’s algorithm is another algorithm used to determine the smallest path tree; its behavior is based on the principle of determining the other edges step by step, starting from a single-sided path tree. There is a path tree consisting of one edge at the beginning, and the selected edges to add to the path tree in the following steps are this path tree. must be adjacent to one of the nodes above it; of course, both ends of the newly selected edge should not be adjacent to more than one node on the path tree. If both ends are adjacent, the tree definition will be exited.
REFERENCES:
- https://www.researchgate.net/figure/Illustration-of-Dijkstras-algorithm_fig1_331484960
- https://commons.wikimedia.org/wiki/File:Depth-First-Search.gif
- https://www.researchgate.net/figure/Example-solved-using-the-Kruskal-algorithm-the-numbers-represent-the-weight-of-each-edge_fig2_338723595
- https://www.javatpoint.com/graph-algorithms
